Jun 07, 2010
Originally posted in the Critical Literacies course blog, June 7, 2010 Change is with us every day. Life would not be possible without it. Change may seem chaotic and unpredictable, but most change occurs in patterns that we can see and recognize. This post isn't an attempt to be the final word on patterns of change. Rather, it is an attempt to introduce the idea and encourage people to think systematically about it. Linear Change Think about a car driving along the highway. Its position is changing every minute, every second. If the driver stays at a constant speed, then its position changes at a steady pace. Driving at 60 mph, for example, the car will travel at one mile per minute. After one minute, it has travelled one mile. After 10 minutes, 10 miles. After 60 minutes – one hour – 60 miles. This is linear change. It is change that occurs at a static pace. If represented on a graph, it would look like this:
Linear Change
Notice that the graph is a straight line. That is why we call this linear change. There are many examples of linear change in your every day life. For example, if water runs steadily from a tap, the pot fills up at a constant rate. Or for example, if a new brick is added to a wall every 30 seconds, then the wall will grow at a linear rate. A significant proportion of educational theory is based on some sort of linear change. Here's an example from a blog I was reading today:
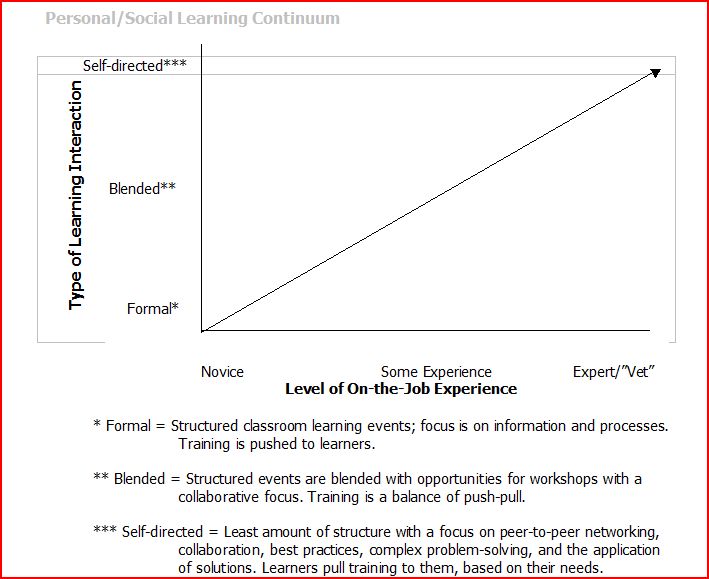
Personal Social Learning Continuum - source: aLearning Blog
It is typical to think of student progress, or learning progress, or some other sort of progress, as happening in a straight line based on some factor or another. But it would be misleading. Linear change is so common in our lives there is a temptation to think of all change as linear change. It's very easy to be lulled into this. The stock market, for example, seems to rise at a fairly steady rate over a period of time. We come to expect this change, and to count on it. And then we're surprised when it suddenly falls. Or, closer to home, the value of our house rises steadily, year after year. We come to expect this to continue indefinitely, and are not prepared for the day housing prices fall. Or, you are sliding down a hill. This feels a lot like driving or riding a bicycle, so you expect your speed to be constant. But all of a sudden, you are going much faster than you intended. Your rate of change has increased, catching you by surprise. Nothing lasts forever. Things that change at a steady pace may appear to be easy to predict, something you can count on, but eventually something changes – the road ends, your gas runs our, you hit a hill, the water stops running, something – and your linear change becomes something else. A linear change can change in two ways: Acceleration or speeding up - the change can speed up. Something that appeared to change constantly can start changing faster and faster. If you press on the gas while driving a car, for example, your speed will accelerate. Deceleration or slowing down – the change can slow down or even come to a stop. In extreme cases, it can even reverse. If you press on the brake (or hit a wall) while driving, your speed will decelerate.
Acceleration and Deceleration
In general, you can use linear change to make short term predictions, but because linear change tends to change, you need to watch for signs of acceleration or deceleration. Any time a course of action depends on constant, linear change you need to have contingency plans – or back-up plans – for sudden changes. That's why we have seatbelts in cars; it's a contingency, in case the car's speed suddenly slows. That's why we have blowout valves in oil wells; it's a contingency in case the flow of oil suddenly increases. Many of the devices that are restraints or governors of some sort are contingencies, devices intended to deal with unexpected acceleration or deceleration. Exponential Change Sometimes a change keeps in changing. If you keep your foot pressed on the accelerator you go faster and faster, for example. When you are falling, you fall faster and faster. The rabbit population in your back yard grows faster and faster every day. This sort of change is called exponential change. It is change that does not progress at a steady rate, like linear change, but which occurs at a faster and faster rate. To picture exponential change, you can construct a simple mental model by imagining what happens when bacteria cells multiply. A single bacteria cell might divide into two cells once every 20 minutes, for example (this is actually how fast e coli multiplies). This is known as its doubling rate. So, after 20 minutes, we have 2 e coli cells. After 40 minutes, each of those has divided into two, and we have four e coli cells. After an hour, they have divided again, and we have eight e coli cells. In another hour, we have 64 cells. And so on. We're not just adding e coli cells to the mix, we're multiplying them, so the number of cells increases at a faster and faster rate. Here's what it looks like on a graph:
Exponential Change
Today you read a lot of people write that we are experiencing a time of exponential change in our society. This is because the rate of change of different things seems to be happening more and more quickly. World population, for example, has been increasing exponentially. World population was 1 billion in 1800, 2 billion in 1920, 3 billion in 1960 (the year after I was born), 4 billion in 1965, and 6 billion in 2000. The pace of technological change has also been exponential. Moore's Law says that processor power will double once every 18 months. Because this is a multiplier we know that it produces exponential change. Because exponential change can grow so rapidly, we sometimes use a different type of graph to represent it. Graphed, the pace of technology change would look much like the pace of e coli growth depicted above. But this would make it very difficult to represent. So instead, we use that is called a logarithmic graph. Here's a logarithmic graph of Moore's Law:
Moore's Law - Source, Wikipedia
Notice that on the left-hand axis (the Y-Axis, which runs up and down) we count the values not one by one but exponentially – 10, 100, 1000, 10000, and so on. In this type of graph, an exponential change looks like a straight line. This makes it easier for us to understand. Models of progression typically invoke either linear change or exponential change. Consider, for example, the development of society in human history. We progressed from the hunter-gatherer stage to agriculture to industrial and now an information-age society. The very concept of progress has, embedded in it, some notion of constant linear change, whether at a steady rate or an ever-increasing rate. There is a danger to this. As with static linear change, we can come to expect change to continue indefinitely. Consider, for example, the advancement of the stock market. This is what we saw in 2000:
Dow Jones 1928-2000 - Source: Yahoo Finance
This has a few bumps, but it's pretty clearly an exponential change. It was on the basis of this long-term chart that investors were advices to "buy and hold" and "invest for the long term." The fluctuations were minor compared to the overall trend. And so we based the economics of everything from mortgages to retirement accounts to business plans on this sort of long-term growth. But look at the same chart extended to 2010:
Dow Jones 1928-2010 - Source: Yahoo Finance
The exponential change has come to a dead halt. The was a crash after 9-11 and then another crash eight years later as the housing bubble burst. Overall, through the decade, there has been no growth in stock values at all. Other economic indicators have become similarly stagnant. Exponential change can look inevitable when you're in the middle of it. But like linear change, there's always the possibility that the acceleration will decrease and even reverse. When this happens, the results can be even more destructive, because we will have built systems based on constantly accelerating growth, not a steady state or even a decline. Parabolic Change There's an old saying: what goes up much come down. This is a principle we can rely on in many circumstances. Throw a baseball into the air – it will rise higher and higher for a certain time, but eventually it will fall back to earth. This is parabolic change. It represents a situation that is limited in duration or extent, and where the changing factor will return to its origin. It looks like this on a graph.
Parabolic Change
There are many examples of parabolic change. The consumption of a limited resource, such as oil, is a good example. Consumption rises for a while as oil is found and refined. However, at a certain point in time – peak oil – the supply begins to fall, and as a result, our consumption of it begins to slow. Eventually, once all the oil is gone, consumption returns to zero. Another example – interestingly – is the human life. When we are born we have few capacities. Gradually we grow, and get stronger, more agile, and smarter. But this (despite the confidence of youth) does not continue indefinitely. As we age, we slow down, become weaker, and even lose of of our mental abilities. Finally we die, and our capacities return to what they were before we were born, to zero. Arnold Toynbee describes the arc of civilization in this way. Civilizations rise and fall, he writes, in a constant and predictable way. They expand in (more or less) a circular fashion until they grow too large for their infrastructure to support. Then, because of this, they begin to decline. "Things fall apart; the centre cannot hold." Not all such changes need to be a perfect parabola. Things can rise very slowly and fall very quickly – "It takes years to build a good reputation, and only seconds to destroy it" – and an arc can rise and drop sharply.In drama, we sometimes talks about the story arc, and this is typically a type of parabolic change, but is not a nice smooth progression. Consider this arc from Buffy the Vampire Slayer:
Buffy the Vampire Slayer Dramatic Arc - Source: Match-Cut.org
Arcs do not always have to return to their starting point either. Sometimes the rise and fall is itself a type of change. Consider this diagram, the Gartner Hype Cycle:
Gartner Hype Cycle - Source: Wikipedia
What this diagram makes clear is that arcs can be positive or negative – they can create peaks or troughs. And, as mentioned, they can result in a higher end-point than starting point. As such, a change like this is – on the long run – effectively the same as a liner change. We could draw a straight line from the starting point to the end point. It's the same result, even if the journey to get there was a little more exciting. Cycles "The more things change, the more they stay the same." Sometimes it seems that, despite all the change in the world, things stay constant. It's like being on a merry-go-round – you might travel a lot, but all you've done is to go around in circles. Cycles for a large part of many theories of change. "History repeats itself," we are told. "Those who do not learn from history are condemned to repeat it." From the perspective of a single civilization, there seems to be a rise and fall, but from the perspective of history, we see a succession of rise and fall, rise and fall – a great cycle of history. We can, in fact, think of cycles as being like a series of parabolas or arcs. They may be positive or negative, depending on how you look at them. Like this:
Cycles - Source: Doctronics
You may recognize this as a sine wave. What a sine wave describes is the movement of a cycle. If you drew a chalk mark on a tire and rolled the tire, the sine wave would describe the motion of the chalk mark as it rotated around the axis, up and down, as the tire moved forward. Our lives are full of cycles. We breathe in and breathe out. Out heart beats at a regular pace. We go to work and return home again. We wake and we sleep. We can actually recognize cycles in sounds as well as by sight. All audio signals, in fact, are types of cycles. The sine wave depicted above, when implemented in electronics and broadcast though a speaker, becomes a musical note. Like this:
Pitch - Source: Doctronics
Play the sound associated with the wave form above: click here The frequency is the number of times the cycle repeats in a second; the amplitude is how high and low each arc goes. In music, the frequency is the same as the pitch, and the amplitude is the same as the loudness. I wrote last week about Soundation Studio. This is interesting because you can create your own types of waves to create different sounds. The sounds effects generator (the blue box, lower left) can be used to create different types of waves – sine waves, like we've seen above, sawtooth waves, square waves, noise, and more. The point here is that we as humans are very sensitive to cycles. We create them, we repeat them, we have evolved an entire science of mathematics, electronics and music based on the manipulation of cycles. We are very prone to see them in the environment, and to expect to see the cycle repeat itself after a time. And we are justified in this. Nature is filled with cycles, from the orbits of the planets to the rise and fall of the Sun to the flow of water through the ecosystem. Often, we draw the circle, instead of a sine wave, to represent some of these more complex cycles, such as the water cycle.
Water Cycle - Source: Environment Canada
Cycles are like linear changes – it is very easy to become used to them, to become comfortable with them. It is natural to assume that cycles are inherent in nature, that they are an inescapable part of life. We see society move to the left, and see as natural a movement back to the more conservative right. While it is natural to think of a cycle as unending and unchanging, it would be a mistake. A cycle is a type of motion, whether it's a tire on a car, sound waves produced by electronics, or the flow of water through an ecosystem. And there's no such thing as perpetual motion. All motion requires some sort of impetus, some sort of energy to create and sustain it. Change the input, and you change the cycle. The Dialectic The concept of the dialectic has its origin in Hegel and is basically the idea that in a cycle there is a motion forward. Hegel introduced us to the concept of thesis and antithesis – which would be similar to the up and down of a chalk marking, or the back and forth between left wing and right wing in politics. These, together, produce what he called the synthesis, which is the product of their interaction. As van der Veen writes, the dialectic "contains elements of both cyclical and linear change, and thus change is spiral; significant change takes place as an attempt to resolve the accumulation of intolerable contradictions, the unravelling of stresses that are inherent in social life; short term repetitive change but with long term cumulative directional change; processes of change persist but the contents of the processes are changing." Here's a representation of that process:
The Dialectic
This is the origin of the concept of the paradigm shift. According to Thomas Kuhn, science does not progress in a linear fashion, but rather progresses through a series of jumps, called paradigms. Within a paradigm we have what is called 'normal science', but eventually, contradictions, unexplained experimental results, and other problems and questions force the science into a crisis point. Through this crisis, our view of the world is revised, and we adopt new scientific theories, terms and concepts. Another way to depict the same process is to think of a series of parabolas – a cycle – creating a linear change. Like this:
Dialectic Cycles
Viewed from a certain perspective, these aren't cycles any more but spirals. There is a movement around and around, but it is headed in some direction. The cycle may be progressing upward, or it may be progressing downward. Stock market analysts have created mathematical models on forms of the dialectic to predict swings in share values. Here is an example called the Elliott Wave Principle:
Elliott Wave Principle - Source: Forex
Here's another example. The author starts with a basic wave pattern of change, the forming-norming model that has become quite popular:
Forming Norming - Source: McNamee and McNamee
These are then joined to created a full dialectic:
Auditing Dialectic - Source: McNeemee and McNeemee
This creates for us two distinct types of change, virtuous and vicious circles. Wikipedia has pretty good examples of these: Virtuous Circle – "Economic growth can be seen as a virtuous circle. It might start with an exogenous factor like technological innovation. As people get familiar with the new technology, there could be learning curve effects and economies of scale. This could lead to reduced costs and improved production efficiencies. In a competitive market structure, this will probably result in lower average prices." Vicious Circle – "Hyperinflation is a spiral of inflation which causes even higher inflation. The initial exogenous event might be a sudden large increase in international interest rates or a massive increase in government debt due to excessive spendings. Whatever the cause, the government could pay down some of its debt by printing more money (called monetizing the debt). This increase in the money supply could increase the level of inflation." Virtuous and vicious circles are the result of feedback loops. What happens is that the result of one cycle feeds into the next cycle, accelerating its effects. The change is not merely linear, it can be exponential. How this happens, and what causes it to happen, varies. Hegel thought it was the result of the world spirit. Marx thought it was the force of history. Today we explain such effects though principles such as the network effect or the first mover advantage. Vicious and virtual cycles occur in interconnected networks, where we have not only a circle much a much more interconnected web of entities. The result from one cycle feeds into the next cycle. In a network, such effect can result in cascade effects. A disease sweeping through a society, a virus spreading through a computer network, a fashion fad sweeping the nation, an idea, word or meme occupying everyone's thoughts – these are examples of cascade effects. Everything can change, sometimes permanently, as a result of a cascade effect. Cascade effects can be wild, sudden, and hard to predict. We may think that we are in a normal cycle, while behind the things a change is gradually accelerating. Global warming is like that – we experience the warmth of the day, the coolness of night, and the warmth of summer and the coolness of winter, and even the effects of 11-year sunspot cycles, and 30-year climactic cycles. But hidden behind these cycles is a gradual and slowly accelerating increase in the overall temperature, global warming. If we aren't looking for it, we won't notice it at all – until it suddenly and catastrophically spirals out of control. Waves When we think of change as happening to a wide area at once, then instead of cycles we sometimes think of change as happening in waves. Probably the most famous example of this is Alvin Toffler's book The Third Wave. According to Toffler, "The First Wave is the settled agricultural society which prevailed in much of the world… The Second Wave Society is industrial and based on mass… (and) The Third Wave is Post-Industrial Society." It is not always clear what someone means when they talk of a wave. Toffler's waves, for example, have been depicted as a form of exponential change
Third Wave - Exponential View - Source: Harbinger
and as a type of dialectical change
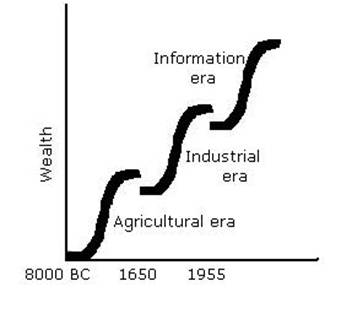
Toffler's Waves - Dialectic - Source: Maaw
The way waves behave can inform us about what to expect from a change, though. Consider how the tsunami spread through the Indian Ocean in 2004:
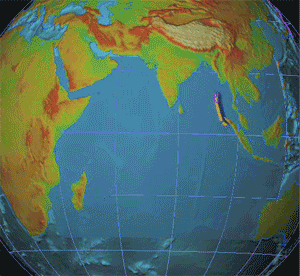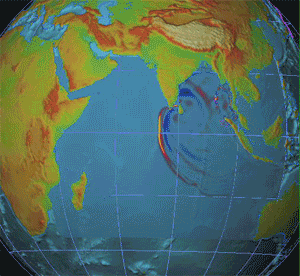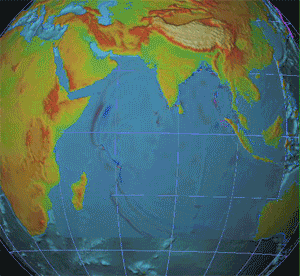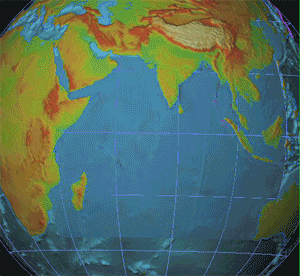
2004 Tsunami - Source: Wikipedia
Waves are not steady and linear. They interact with each other and with landforms around them. Understanding waves involves not only understanding how they propagate but also in understanding these interactions. Consider, for example, how the intersection of two waves can amplify or dampen the wave:
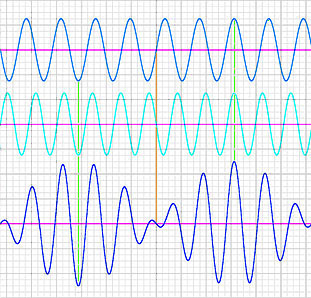
Beat Note - Source: Allan Watson III
Two waves at different frequencies – different pitches – applied on top of each other produce what is called a 'beat note'. This is the result of them amplifying when they are in phase and cancelling each other out when they are out of phase. The same effect happens in the would at large. We sometimes talk about the "stars being aligned" or "the right things coming together". The 60s "Summer of Love" is sometimes described in such terms, as it represented the coincidence of widely available drugs, including the invention of LSD, the sexual revolution, made possible by the birth control pill, and the creation of a new form of music. As you can easily see from the diagram, a confluence of factors can cause effects all out of proportion to what one might expect from the waves on their own. Drivers and Attractors One effect of the wave analogy is to represent change as something that is overwhelming and inevitable. No doubt this is part of the impression Toffler tried to convey with his title. The thought of change as something that cannot be resisted is a common theme in the literature. In a sense, it's true. Change is inevitable. Without change, we would all be static, inert lumps of clay. Our lives and being depend on change. And change happens, every in the world, every minute of the day. As Isaac Asimov says, "It is change, continuing change, inevitable change, that is the dominant factor in society today. No sensible decision can be made any longer without taking into account not only the world as it is, but the world as it will be." Maybe so. But as noted above, no change occurs by itself. All change is a type of motion, and all motion has some sort of impetus or cause. Change does not occur in isolation; something makes it happen. We sometimes represent these as drivers and attractors. These are a bit like push and pull. A driver is some force or energy behind the change, pushing it forward. An attractor is something in front of the change, pulling it forward. You see references to drivers in a lot of political and economic literature. Drivers are often depicted as external forces that push economic or social behaviour in a certain direction. Consider this diagram, for example:
Drivers of Change - Source: Alagse
Here we see three major drivers depicted: ICTs, globalization, and climate change. We see that these drivers are pushing us toward operational; efficiency, size and competitiveness, and sustainability. These drivers are depicted in a variety of ways. Here we have sort of a flow chart:
Driver Flow Chart - Source: Gecafs
Again, the use of drivers is as causes that almost force the outcome. It's as though the authors are intending to say, "Given these forces in the world, we cannot help but to change in such and such a way." Attractors are a bit different. Attractors are like gravity: they pull us toward some sort of goal or destination. While drivers seem to force us toward some sort of linear change, attractors seem to pull us in cycles. The spiral-based change typically revolves around an attractor. An attractor need not be physical, like gravity. It can also be an objective or goal. While such attractors can motivate change, they can't really be said to cause change – they require human agency for that. Here's an example of such an attractor:
Semantic Attractor - Source: Peter Hale
In this case, the attractor is that sweet spot at the intersection of programming, modelling and the semantic web. Whatever it is that's in there is pulling in the programmer toward it over time. Here's another example, depicting development toward some military objective. This time the spiral goes up:
Military Attractor - Source: Mitre
Theories of change need to take into account the attractors as well as the drivers. Understanding what motivates people is as important as what urges and needs they have. An understanding of this would better inform educational theory. In education, people are thought to learn according to different learning styles. A person might learn better by reading, listening, looking at pictures, or working with his or her hands. But studies of educational outcomes based on learning styles are inconclusive. There doesn't seem to be an improvement in learning even if the teacher adapts to a student's learning style. But in education, a student's motivation is just as important. Teachers need to adapt not just how they push students toward learning, but how they attract them. A student has to be ready to learn, wanting to learn, and able to overcome the anxiety of learning. Different theories of motivation attempt to explain what attracts people to certain kinds of change. Design and Selection In many kinds of change, the result of the change is defined not simply by a process but also by a logic. The changing image on your computer screen, for example, is not the result of natural forces, but because of a specific design. This is reflective of the impact choice has on change. At any moment in time you and about 6 billion other people – not to mention billions of other animals and insects – are making choices about what to do or say next. Should I finish writing the paper? Stay up late? Drink a beer? In computers, changes of state are represented by flow charts. These charts describe the decisions the software makes – often based on user input – in order to produce a result. But flow charts need not only describe software decisions. They can describe human actions as well. For example, should you change the lamp?
Flow Chart - Source: Wikipedia
But how do people actually make decisions? In many cases, they are not rational – they do not compute results like a computer, but rather follow their own sometimes irrational beliefs and inclinations. A great deal of theory supposes that people are rational agents – and this supposition is often the cause of error. There are many types of rational behaviour, and not all are instrumentalist or goal-directed. Moreover, not all choice is made by humans or rational agents. Animals, plants and even inanimate objects enter into points of decision. These choices may be bounded by the nature and situation of the the chooser, but are in other cases quite random and impossible to predict. Will the deer on the highway veer right or left? Will the rock land on the road or roll off to the side. Will this uranium atom decay today or a dozen years from now? Genetics, evolution, and similar natural processes are the result of these factors. This is not the place to discuss these in detail. But it is important to take into account that this do not stay the same, that they evolve and adapt, as a result of forces such as natural selection. Expecting the bacterium to stay the same, expecting the opposing football team to play the same – these would be mistakes, based on a failure to recognize the influence of adaptation. Finally, as suggested above, some changes are genuinely chaotic and random. The outcome cannot be predicted – it depends on factors that may be too small to be measured or simply unknown to science. In such a case, the graph of the future is not a line, but rather, splits up to define a probability space. This is the classic diagram of chaotic change:
Chaos - Source: Wikipedia
Change progresses on a line for a period of time, then divides into two possibilities, then four, and then an almost infinite number.But note that even in a chaotic system, there is a range of possibilities. It's like predicting the weather – we might not be able to predict it exactly, but we know it will be warmer in the summer and colder in the winter. Patterns of Change This has been an overview of different types of change. It is by no means a complete description of change. At best, it is an introduction. But the main intent of this post is not to describe and explain the different types of change. You can find more detailed and more authoritative treatments in mathematics texts, economics and business texts, and history texts. Indeed, almost any discipline will have its own treatment of change. The purpose of this article has been to make it clear that it is possible to think systematically about change, and that it is fairly easy to recognize different types of change. Almost every theory you encounter in any discipline will appeal to one of the theories of change described above. Knowing that these theories have properties – and strengths, and weaknesses – in common helps you understand them and to criticize them.
